7 - Übungen - 1.12.17

Source

Vektorielles Rechnen in Numpy

Grundrechenarten

Eindimensional

Gegeben sind zwei Arrays

In [1]:
import numpy as np


arr1 = np.array([1, 2, 3])
arr2 = np.array([5, 6, 7])

Bilden Sie die Summe, Differenz, das Produkt, etc..

In [2]:
arr1 + arr2
arr1 - arr2

# usw.
Out[2]:
array([-4, -4, -4])

Was passiert, wenn Sie statt arr2, eine einzelne Zahl (num = 5) benutzen?

In [3]:
arr1 + 5

# geht auch. [1, 2, 3] + 5  entspricht [1, 2, 3] + [5, 5, 5]
Out[3]:
array([6, 7, 8])

Zweidimensional

Diesmal ist eine Matrix gegeben

In [4]:
arr_2d = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])
  • Addieren (subtrahieren, ...) Sie eine einzelne Zahl
In [5]:
# arr_2d + 5 entspricht arr_2d + [[5, 5, 5], [5, 5, 5], [5, 5, 5]]
  • Addieren (subtrahieren, ...) Sie einen Vektor der Länge 3. Was passiert?
In [6]:
# arr_2d + [1, 2, 3] entspricht arr_2d + [[1, 2, 3], [1, 2, 3], [1, 2, 3]]
  • Wie muss der Array aussehen, den man auf arr_2d addiert, damit das Ergebnis
array([[ 2,  3,  4],
       [ 6,  7,  8],
       [10, 11, 12]])

ist? (Tipp: Spaltenvektor!)

In [7]:
arr = np.array([[1], 
                [2], 
                [3]])

print(arr_2d + arr)

[[ 2  3  4]
 [ 6  7  8]
 [10 11 12]]

Reshape

Oft ist es hilfreich, die Elemente eines Arrays anders anzuordnen. So kann man z.B. aus einem eindimensionalen Array der Länge 15, einen zweidimensionalen Array mit der Shape (3, 5) machen (drei Zeilen, fünf Spalten).

In [8]:
arr_1d = np.arange(15)
arr_2d = arr_1d.reshape((3, 5))

  • Machen Sie aus arr_2d einen Array mit fünf Zeilen und drei Spalten!

  • ... mit fünfzehn Zeilen und einer Spalte

  • einer Zeile und fünfzehn Spalten

  • einen eindimensionalen Array

In [9]:
print("5x3:", arr_2d.reshape((5, 3)))

print("15x1:", arr_2d.reshape((15, 1)))

print("1x15:", arr_2d.reshape((1, 15)))

print("1D:", arr_2d.reshape(15))

5x3: [[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]
 [12 13 14]]
15x1: [[ 0]
 [ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]
 [13]
 [14]]
1x15: [[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]]
1D: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]

Slicing

Eindimensional

Gegeben ist ein Array aus zwanzig Elementen

In [10]:
arr = np.array(list("abcdefghiklmnopqrstuvwxyz"))

Lassen Sie sich die ersten 10 ausgeben (Die Syntax fürs Slicen ist wie bei Python-Listen)

In [11]:
arr[:10]
Out[11]:
array(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'k'],
      dtype='<U1')

Zweidimensional

Diesmal ist ein zweidimensionaler Array mit vier Zeilen und fünf Spalten gegeben.

In [12]:
arr2d = arr[:20].reshape((4, 5))
print(arr2d)

[['a' 'b' 'c' 'd' 'e']
 ['f' 'g' 'h' 'i' 'k']
 ['l' 'm' 'n' 'o' 'p']
 ['q' 'r' 's' 't' 'u']]

Man kann auch in zwei (oder mehr) Dimensionen slicen. Beispiel:

In [13]:
print(arr2d[:2, :2])

[['a' 'b']
 ['f' 'g']]

Benutzen Sie Slicing, um

  • die letzten drei Elemente der vorletzten Zeile auszugeben ("n", "o", "p")

  • den Ausschnitt [["g", "h"], ["m", "n"]] zu bekommen

In [14]:
print(arr2d[-2, -3:])

print(arr2d[1:3, 1:3])

['n' 'o' 'p']
[['g' 'h']
 ['m' 'n']]

Schwerpunktsberechnung

Gegeben sind die Koordinaten von drei Atomen, sowie deren Massen

In [15]:
position_atom1 = [0, 0, 0]
position_atom2 = [2.5, 4, 1.3]
position_atom3 = [8, -3, 7.5]


masses = np.array([0.5, 1.3, 2.7])


atoms = np.array([position_atom1,
                  position_atom2,
                  position_atom3]
                 )

Der Schwerpunkt der Atome wird berechnet, indem jede Atomposition mit der zugehörigen Masse multipliziert wird. Anschließend wird der resultierende Vektor durch die Gesamtmasse geteilt.

  • Benutzen Sie reshape, um masses zu einem Spaltenvektor zu machen

  • Multiplizieren Sie atoms mit masses, und addieren Sie die Vektoren entlang der nullten Dimension

  • Teilen Sie durch die Summe von masses

In [16]:
np.sum(atoms * masses.reshape((3, 1)), axis=0) / masses.sum()
Out[16]:
array([ 5.52222222, -0.64444444,  4.87555556])

Monte Carlo

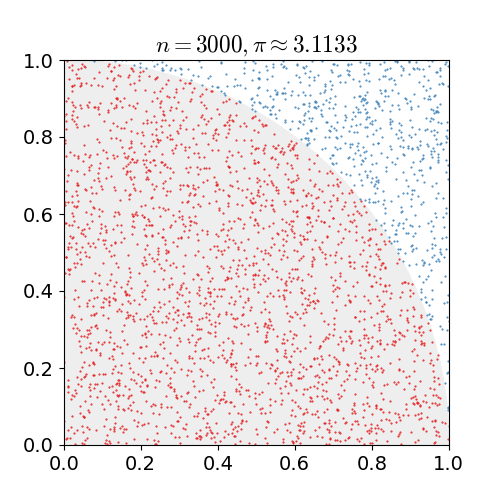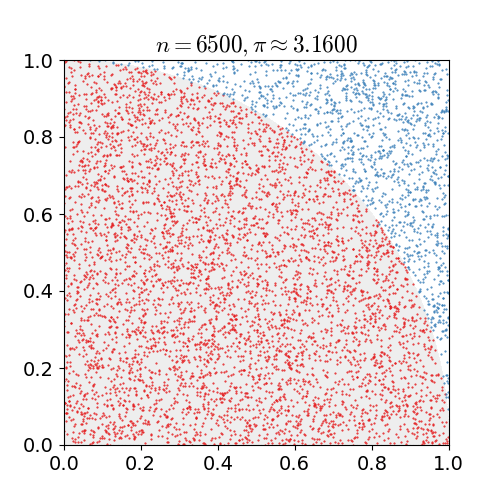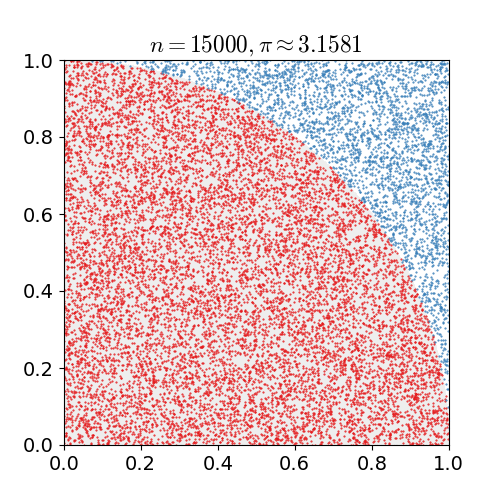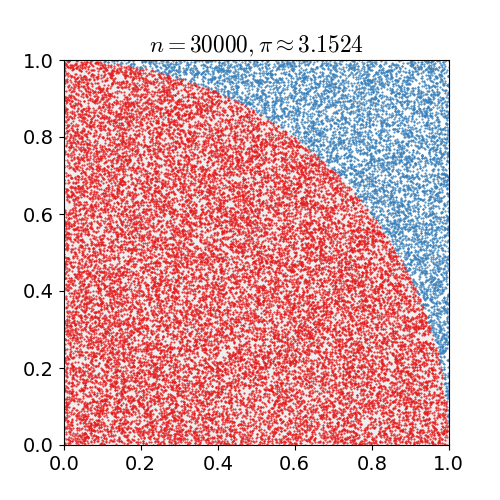
PI_Berechnung

Quelle: https://en.wikipedia.org/wiki/Monte_Carlo_method

Bestimmen Sie die Kreiszahl \(\pi\), indem Sie zufällig Punkte in einem Koordinatensystem der Länge 1 und Höhe 1 verteilen. Wenn Sie einen Kreis ziehen, dessen Zentrum im Ursprung des Koordinatensystems liegt, ist ein Viertel davon in dem Koordinatensystemausschnitt zu sehen. Einige der zufällig gewählten Punkte werden nun innerhalb des Viertelkreises liegen, andere außerhalb. Bestimmen Sie über das Verhältnis \(\frac{\text{Anzahl der Punkte im Kreis}}{\text{Gesamtanzahl der Punkte}}\) die Zahl \(\pi\).

Hinweis: Mittels

np.random.random(shape)

können Sie einen Array mit Zufallszahlen im Intervall [0, 1) erzeugen.

In [17]:
# Idee: generiere zufällig eine Koordinate im Quadrat und prüfe, ob sie im Kreis liegt oder nicht.
# Das Verhältnis Punkte im Kreis / Gesamtzahl Punkte sollte dem Verhältnis Kreisfläche / Gesamtfläche entsprechen

# Vorgehen bei einem einzelnen Punkt:

# Punkt erzeugen
x = np.random.random()
y = np.random.random()

# Prüfen, ob er im Kreis liegt
print(x**2 + y**2 <= 1)


# Jetzt das selbe für viele Punkte auf einmal:
gesamtanzahl_punkte = 10000
x = np.random.random(gesamtanzahl_punkte)
y = np.random.random(gesamtanzahl_punkte)

# Prüfen, ob er im Kreis liegt
print(x**2 + y**2 <= 1)


# Jetzt müssen wir nur noch die Trues in dem Array zählen
# Wir nutzen dafür aus, dass True intern als 1 gespeichert wird, und False als Null

anzahl_punkte_im_kreis = np.sum(x**2 + y**2 <=1)
print(anzahl_punkte_im_kreis / gesamtanzahl_punkte)

print("Schätzung für Pi:", anzahl_punkte_im_kreis / gesamtanzahl_punkte * 4)

True
[ True False  True ...,  True  True  True]
0.7805
Schätzung für Pi: 3.122

Apfel-Männchen

Gegeben ist eine rekursive Folge für komplexe Zahlen

\(z_{i+1} = z_i^2 + c \)

mit \(z_0 = 0\)

Je nachdem wie man c wählt, bleibt diese Folge beschränkt (d.h. der Betrag der komplexen Zahl (np.abs) bleibt unter einer gewissen Grenze), oder sie divergiert.

1) Erstellen Sie einen komplexen 2D-Array c, der die komplexe Ebene darstellen soll. Der Realteil soll dabei von -2 bis 2 verlaufen, der Imaginärteil von -i bis i. Dies erreichen Sie durch folgende Schritte:

  • Erstellen Sie einen Float-Array für den Realteil und einen für den Imaginärteil:
real = np.linspace(-2, 2, 100)
imag = np.linspace(-1, 1, 50) * 1j
  • Um ein zweidimensionales Gitter zu erstellen, schreiben Sie folgendes:
R, I = np.meshgrid(real, imag)
c = R + I

c ist nun ein zweidimensionales Array, das die Punkte der komplexen Ebene zwischen -2-1j und 2+2j enthält.

2) Erstellen Sie einen komplexen Array z, sowie einen Integer-Array counter, die beide die selbe shape wie c haben

z = np.zeros_like(c, dtype=complex)
counter = np.zeros_like(c, dtype=int)

3) Nun beginnt die Hauptschleife: berechnen Sie in 100 Schritten die Werte z_1 bis z_100, indem Sie ihren Array z immer wieder neu berechnen. Überprüfen Sie nach jeder Rechnung, welche Elemente des z-Arrays noch einen Betrag (np.abs) kleiner 10 haben (-> den resultierenden Boolschen Array können Sie zu counter hinzuaddieren. True wird dann als Wert 1, und False als Wert 0 aufgefasst).

4) Zum Schluss können Sie sich ein Bild des Counters ausgeben lassen. Dazu müssen Sie zu Beginn des Skripts folgendes Paket importieren:

from PIL import Image

anschließend können Sie mit folgenden 3 Zeilen ein Bild speichern:


counter = np.array(counter/100. * 255, dtype=np.uint8)
img = Image.fromarray(counter)
img.save("mandelbrot.png")

5) Experimentieren Sie auch mit anderen Grenzen des Arrays c. Sie können so weiter in das Apfelmännchen "zoomen".

In [39]:
plt.figure(figsize=(20, 10))

real_min, real_max = -2, 1
imag_min, imag_max = -1, 1

cols = 1200
lines = int((imag_max - imag_min) / (real_max - real_min) * cols)

real = np.linspace(real_min, real_max, cols)
imag = np.linspace(imag_min, imag_max, lines) * 1j
R, I = np.meshgrid(real, imag)
c = R + I
z = np.zeros_like(c, dtype=complex)
counter = np.zeros_like(c, dtype=int)

threshold = 10

for _ in range(100):
    below_threshold = z < threshold
    z[below_threshold] = z[below_threshold]**2 + c[below_threshold]
    counter[below_threshold] += 1

#counter = np.array(counter / 100 * 255, dtype=np.uint8)
plt.imshow(counter, extent=[real_max, real_min, imag_max, imag_min])
plt.savefig("test.png")

/scratch/kabbe/programs/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:20: RuntimeWarning: overflow encountered in square
/scratch/kabbe/programs/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:20: RuntimeWarning: invalid value encountered in square
In [38]:
In [ ]: