6 - Scipy & Matplotlib

Plotten mit Matplotlib

1D-Plots

Siehe auch offizielles Tutorial von der matplotlib-Seite

Simples Beispiel

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [1, 2, 3, 4, 5]

plt.plot(x, y)
plt.show()

Resultat ist dann diese Linie:

Möchten wir, dass Matplotlib keine durchgezogene Linie zeichnet, geben wir der plot-Funktion noch folgendes Argument mit:

plt.plot(x, y, 'o')

Dann plottet Matplotlib nur die einzelnen Datenpunkte, ohne sie miteinander zu verbinden:

Das letzte Argument ist der Formatstring. Mit diesem können wir Farbe, Punkt- und Linienstil bestimmen.

Aufgabe:

Benutzen Sie

help(plt.plot)

um mehr über die möglichen Formatoptionen zu erfahren. Zeichnen Sie das obige Beispiel mit

• einer grünen gestrichelten Linie

• einer gelben durchgezogenen Line und Dreiecken für die Datenpunkte

Funktionen plotten

Numpy macht es uns einfach, mathematische Funktionen zu plotten. Zuerst überlegen wir uns, in welchem x-Bereich wir plotten wollen. Wir nehmen hier als Beispiel den Bereich von \(-2 \pi\) bis \(2 \pi\) Mithilfe von np.linspace können wir nun einen Array mit oben genannten Grenzen erstellen:

x = np.linspace(-2*np.pi, 2*np.pi)

Per Default erzeugt linspace einen Array mit 50 Datenpunkten. Wir können aber als drittes Argument auch eine andere Zahl von Datenpunkten festlegen.

Dank Numpys vektorisierbaren Funktionen, können wir die gewünschte mathematische Funktion, z.B. einen Sinus, einfach auf den x-Array anwenden und erhalten so die zugehörigen y-Werte:

y = np.sin(x)

Jetzt müssen wir das ganze nur noch plotten:

plt.plot(x, y, "--")
plt.show()

Das Ergebnis ist ein Sinus mit zwei Perioden:

Achsen beschriften

Achsenbeschriftungen fügen wir hinzu mittels:

plt.xlabel("Time / seconds")
plt.ylabel("Amplitude / meters")
plt.plot(x, y)
plt.show()

Latex-Formeln können übrigens eingebunden werden, indem man sie zwischen zwei Dollar-Zeichen schreibt.

Subplots

Manchmal kann es hilfreich sein, ein paar Schaubilder gleich in einem Plot unterzubringen. Wenn wir uns z.B. die Schwingung eines Pendels anschauen, ist es hilfreich, ein Schaubild für die momentane Position des Pendels, und ein weiteres für seine Geschwindigkeit zu plotten. Mithilfe des Befehls subplot können wir matplotlib mitteilen, wieviele subplots wir neben- und wieviele übereinander wir haben möchten.

import matplotlib.pyplot as plt
import numpy as np

time = np.linspace(0, 2*np.pi)
amplitude = np.sin(time)
velocity = np.cos(time)

# Erster Parameter: Anzahl der Zeilen der "Plot-Matrix"
# Zweiter Parameter: Anzahl der Spalten der "Plot-Matrix"
# Dritter Parameter: Nummer des Plots
plt.subplot(2, 1, 1)
plt.plot(time, amplitude)
plt.xlabel("time / seconds")
plt.ylabel("amplitude / meters")

plt.subplot(2, 1, 2)
plt.plot(time, velocity)
plt.xlabel("time / seconds")
plt.ylabel("velocity / ms$^{-1}$")

plt.show()

Ergebnis:

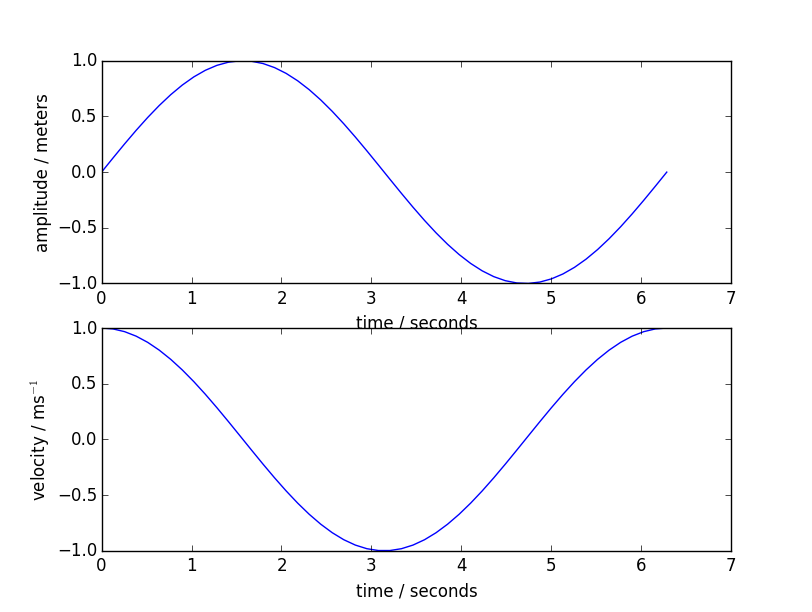
Die Argumente, die wir subplot mitgeben sind die Anzahl der Zeilne und die Anzahl der Spalten der subplot-Matrix, sowie die Nummer des aktuellen subplots, den wir bearbeiten. In unserem Beispiel kreieren wir zwei subplots in einer Spalte (daher 2, 1).

Aufgabe:

• kreieren Sie drei Subplots in einer Zeile

Histogramme

Auch Histogramme lassen sich sehr komfortabel in matplotlib erstellen. Als Beispiel machen wir mal wieder etwas Buchstaben-Statistik:

import matplotlib.pyplot as plt
import numpy as np
from collection import Counter

text = "Beliebiger Beispieltext um einige Buchstaben für unser Histogramm zu bekommen"
c = Counter(text.lower())

counts = c.values()
plt.hist(counts, bins=np.arange(min(counts)-0.5, max(counts)+1.5))
plt.xlabel("Vorkommen im Text")
plt.ylabel("Anzahl Buchstaben")
plt.show()

mit dem Ergebnis

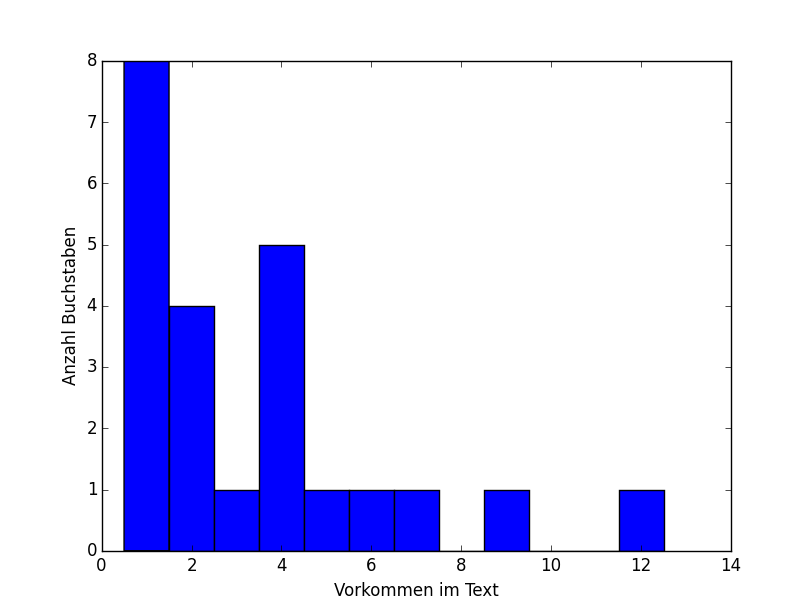
Wir sehen also, dass 8 Buchstaben nur ein einziges Mal im Text auftauchen, und es nur einen einzigen Buchstaben gibt, der 12 Mal im Text erscheint.

Text in Schaubilder einfügen

Möchten wir im obigen Beispiel z.B. kenntlich machen, dass der einzelne Buchstabe, der im gesamten Text zwölfmal vorkommt, der Buchstabe "e" ist, können wir das folgendermaßen machen.

Vor plt.show() schreiben wir noch:

plt.text(12, .5, "e", fontdict=dict(color="red", fontsize=25))

Mit dem Ergebnis

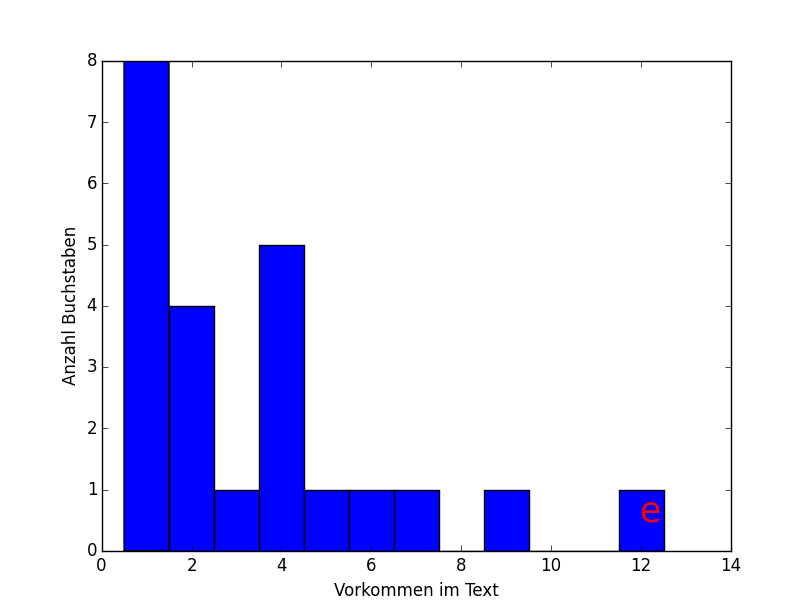
Damit wird an die Koordinate 12, 2 in unserem Schaubild der Buchstabe "e" geschrieben.

Möchten wir einen Pfeil benutzen, um auf den zugehörigen Balken zu zeigen benutzen wir statt plt.text plt.annotate:

plt.annotate("Buchstabe 'e'", xy=(12, 1), xytext=(10, 3.5),
             arrowprops=dict(facecolor='black', shrink=0.05))

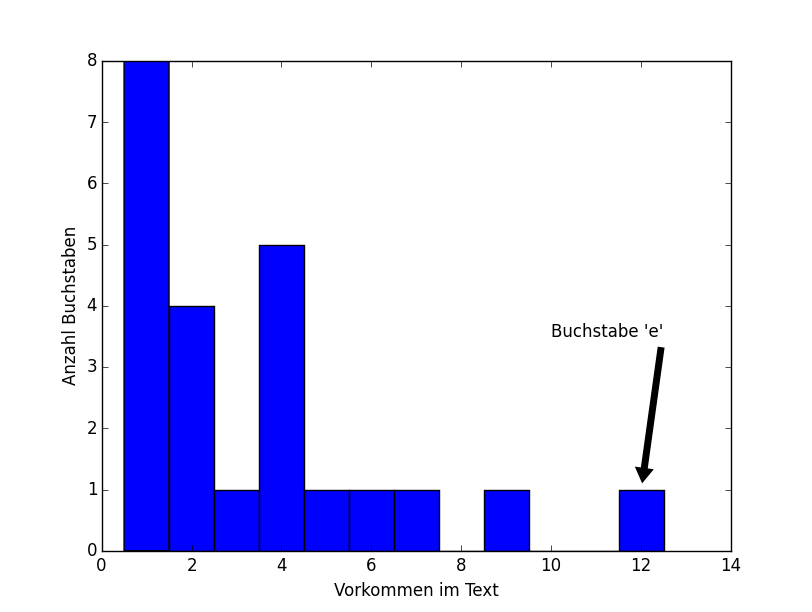
Logarithmische Achsen

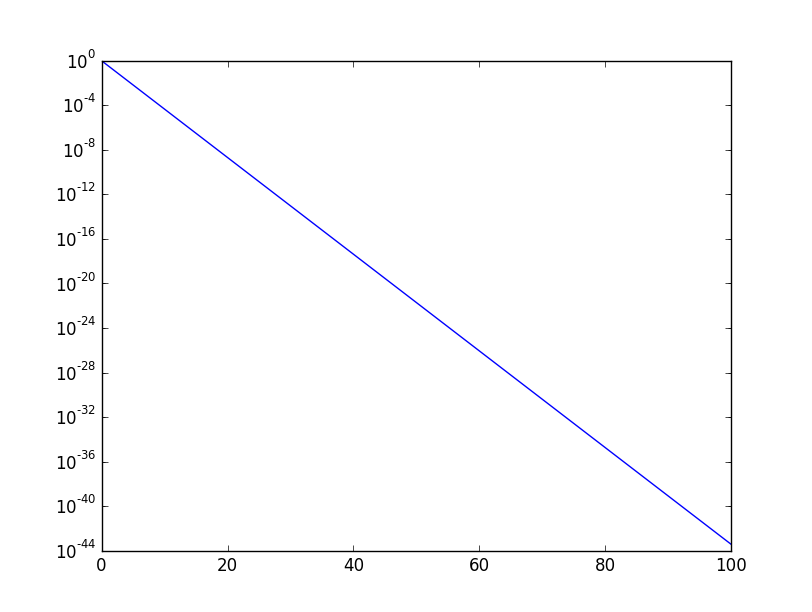
Beim Plotten von exponentiellen Funktionen, sind halblogarithmische Darstellungen sehr hilfreich. In matplotlib lässt sich das mithilfe von xscale oder yscale einstellen.

x = np.linspace(0, 100)
y = np.exp(-x)

plt.yscale("log")
plt.plot(x, y)
plt.show()

Fehlerbalken

Haben wir Datenpunkte mit Fehlerintervallen, können wir diese mittels plt.errorbars plotten:

x = np.linspace(0, 10)
y = 3*x + np.random.uniform(-3, 3, size=x.shape)
y_err = 5.0
plt.errorbar(x, y, y_err)
plt.show()

Ergebnis:

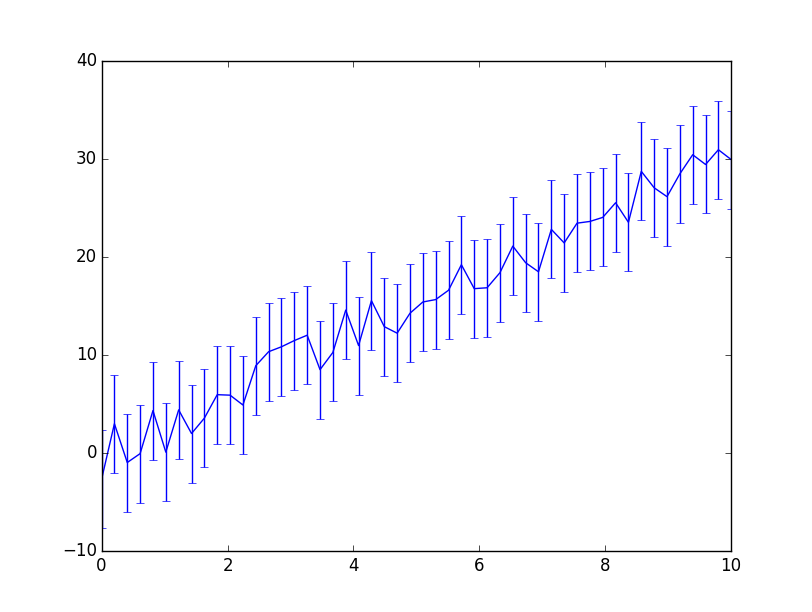
y_err darf auch ein Array mit der gleichen Länge wie x und y sein.

3D Plots

http://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html

Numerik mit Numpy & Scipy

Optimierungsprobleme

Unter scipy.optimize finden sich diverse Funktionen, mit denen man Maxima/Minima von mehrdimensionalen Funktionen bestimmen kann

Least-Squares-Fitting

Das vermutlich häufigste Optimierungsproblem ist das Fitten einer Funktion an Messpunkte. Dabei sucht man für eine gegebene Funktion die Parameter, die die Abweichung der Funktion zu den Messwerten minimiert.

Scipy bietet dafür die Funktion curve_fit an.

Als Eingabe erwartet curve_fit die Funktion, die an die Messdaten gefittet werden soll, sowie die Messwerte als x- und y-Werte.

Beispiel 1: Lineares Fitten:

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit


x = np.linspace(0, 10)
# wir simulieren uns unsere eigenen Messwerte, indem wir eine lineare Funktion mit leichtem Rauschen versehen
y = 3*x + np.random.uniform(-3, 3, size=x.shape)


# Unsere Fit-Funktion ist eine Gerade mit Steigung m und y-Achenabschnitt y_0
def fit_function(x, m, y_0):
    return m*x + y_0

parameters, covariance_matrix = curve_fit(fit_function, x, y)

m, y_0 = parameters

plt.plot(x, y, "x", label="Messwerte")
plt.plot(x, m*x+y_0, label="Fit")
plt.legend(loc="upper left")
plt.show()

Das Ergebnis sieht dann so aus:

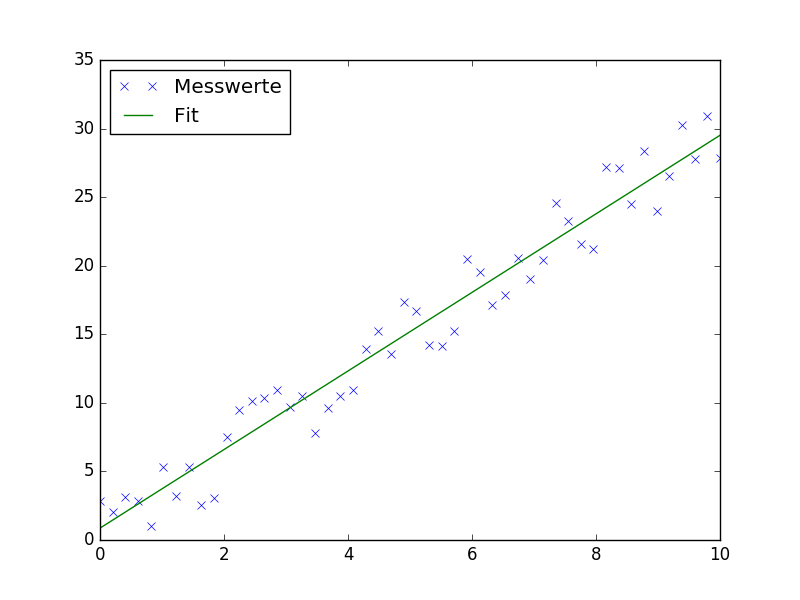
Als kleines Feature wurde jedem Plot noch ein Label mitgegeben, und anschließend eine kleine Legende hinzugefügt.

Auch kompliziertere, nichtlineare Funktionen lassen sich fitten: In diesem Beispiel erzeugen wir leicht verrauschte Sinus-Pseudomessdaten und versuchen per Fit die Parameter zu bestimmen.

x = np.linspace(-2*np.pi, 2*np.pi)
y = 3.5 * np.sin(1.7*x) + np.random.uniform(-1, 1, size=x.shape)

def fit_func(x, a, omega):
    return a*np.sin(omega*x)

(a, omega), _ = curve_fit(fit_func, x, y)
plt.plot(x, y, 'x')
plt.plot(x, fit_func(x, a, omega))
plt.show()
print(a, omega)

Das Resultat lässt leider noch zu wünschen übrig:

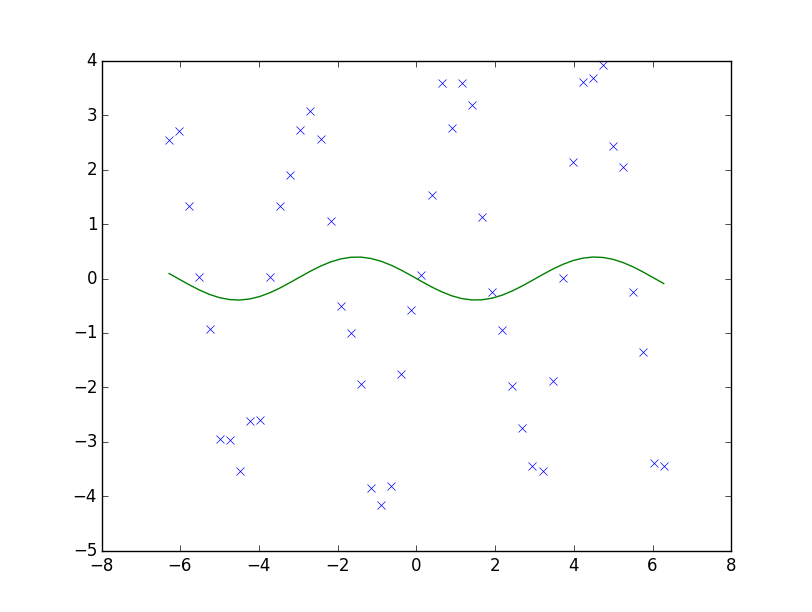
und unsere erhaltenen Parameter sind a = -0.736183524681 und omega = 1.03897143312.

Die Resultate von nichtlinearen Fits hängen leider oft stark von den "initial guesses" der Parameter ab!

Wenn wir aber der curve_fit Funktion mittels p0 noch bessere Startparameter mitgeben:

(a, omega), _ = curve_fit(fit_func, x, y, p0=[3.0, 1.3])

schafft es der Algorithmus besser, das Minimum der Summe der Fehlerquadrate zu finden, und wir erhalten die Parameter a = 3.54570144344 und omega = 1.6905459317.

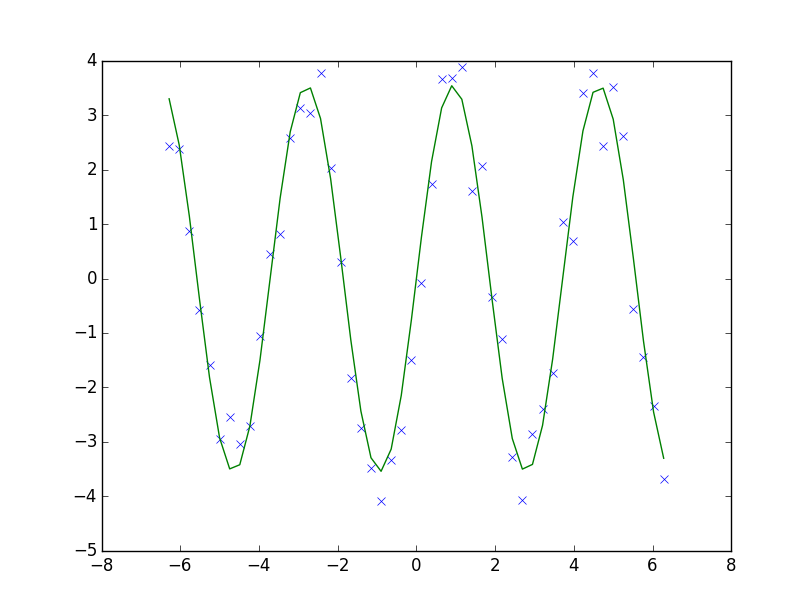
Ein Blick in die Dokumentation